특성 공학과 규제
- 특성 공학(Feature Engineering) : 머신러닝 모델의 성능을 향상시키기 위해 원본 데이터를 변형하거나 새로운 특성을 생성하는 과정.
- 주요 기법
- 다항 특성 생성 : 데이터의 비선형 관계를 포착하기 위해 입력 변수의 제곱, 세제곱 등의 다항식 변수를 추가하는 기법.
- 표준화(Standardization)와 정규화(Normalization)
- 표준화 : 평균이 0이고 분산이 1이 되도록 데이터를 변환해서 모델이 특정 변수에 치우치지 않게 한다.
- 정규화 : 데이터의 스케일을 0 ~ 1 범위로 변환해서 학습을 안정적으로 만든다.
- 불필요한 특성 제거 : 상관관계가 낮거나, 중요도가 낮은 특성을 제거해서 과적합을 방지하고, 학습 속도를 향상시킨다.
- 차원 축소 : 고차원의 데이터를 저차원으로 변환하여 학습 속도를 높이고 과적합을 방지한다.
- 주요 기법
- 머신러닝에서의 규제(Regularization) : 머신러닝 모델이 과적합 되는 것을 방지하기 위해 모델의 복잡도를 줄이는 기법.(ex - 선형 회귀, 로지스틱 회귀, 신경망 등)
- 특성 겅학과 규제의 관계
- 특성 공학을 활용하면 규제 없이 과적합을 방지할 수 있음.
- 특성이 많아지면 과적합 가능성이 커지기 때문에 규제를 함께 사용해서 모델을 단순화하는 것이 중요.
- 일반적으로 다항 특성을 추가함녀 모델이 복잡해질 수 있으므로 다양한 규제를 적용해서 과적합을 방지.
데이터 준비

import pandas as pd
df = pd.read_csv('https://bit.ly/perch_csv_data')
perch_full = df.to_numpy()
print(perch_full)- df = pd.read_csv('https://bit.ly/perch_csv_data') : CSV 파일을 불러와 데이터프레임으로 변환
- perch_full = df.to_numpy() : 데이터프레임을 넘파이 배열로 변환


# 타깃 데이터 생성은 동일
import numpy as np
perch_weight = np.array(
[5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0,
110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0,
130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0,
197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0,
514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0,
820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0,
1000.0, 1000.0]
)# 입력 데이터를 훈련 세트와 테스트 세트로 분리
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
perch_full, perch_weight, random_state = 42)
PolynomialFeatures 다항 특성 변환
입력 데이터를 다항식 형태로 변환하는 기능 제공.

PolynomialFeatures()의 기본값 degree = 2 : 2차 다항식 변환.
입력 데이터 X = [2, 3]
| 변환된 특성 | 계산 값 |
| 1(절편) | 1 |
| x₁ | 2 |
| x₂ | 3 |
| (x₁)² | 2² = 4 |
| x₁ x₂ | 2 x 3 = 6 |
| (x₂)² | 3² = 9 |

농어 입력 데이터에 적용하기
# 훈련 데이터에 대해 변환
poly = PolynomialFeatures(include_bias = False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
print(train_poly)

테스트 세트 변환

다중회귀 모델 훈련 및 점수 확인
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
이 데이터를 이용해서 선형 회귀 모델 훈련
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(train_poly.shape)
특성값 표준화
- 특성의 스케일이 정규화되지 않으면 곱해지는 계수의 차이가 남.
>>> 선형 회귀 모델에 규제를 적용할 때 공정하게 제어되지 않음.
# StandardScaler()를 이용해서 특성을 표준점수로 변환
# 변환기의 사용 방법 : fit()->transform()
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_poly)
train_scale = ss.transform(train_poly)
test_scale = ss.transform(test_poly)- StandardScaler() : 데이터의 평균을 0, 표준 편차를 1로 변환하는 표준화(정규화) 기법.
- 다항 회귀에서는 x^2, x^3 등의 특성이 추가되면서 값의 범위가 커지기 때문에, 특정 특성이 너무 큰 영향을 주는 것을 방지하기 위해 표준화가 필요하다.
표준점수에 사용한 평균값과 표준 편차 확인하기

선형 회귀 모델에 규제를 추가한 모델
- 릿지(Ridge)와 라쏘(Lasso)
- 릿지(Ridge)
- 선형 회귀에 L2 규제를 추가한 모델
- L2 규제 손실함수 = MSE + α x (모든 계수의 제곱 합)
- α 값이 클수록 가중치가 0에 가까워지고, 모델이 단순해짐
- 라쏘(Lasso)
- 선형 회귀에 L1 규제를 추가한 모델
- L1 규제 손실함수 = MSE + α x (모든 계수의 절댓값 합)
- 일부 가중치를 0으로 만들어 불필요한 특성을 제거
| 비교 | 릿지 회귀(Ridge) | 라쏘 회귀(Lasso) |
| 규제 방식 | L2 규제 | L1 규제 |
| 효과 | 가중치 크기 감소(0에 가깝게) | 가중치 중 일부를 0으로 만들어서 특성 제거 |
| 과대적합 방지 | 가능 | 가능 |
| 특성 선택 | X (모든 특성 사용) | O (불필요한 특성 자동 제거) |
| 다중 공선성 해결 | 가능 | 가능 |
| 사용 사례 | 모든 특성이 중요한 경우 | 특성이 많은 경우(고차원 데이터) |
- 특성이 모두 중요할 때 == 릿지 회귀
- 불필요한 특성이 만을 때 == 라쏘 회귀
- 릿지 회귀와 라쏘 회귀를 동시에 적용한 모델 == 엘라스틱넷
1. 릿지 회귀 모델

선형 회귀에서의 점수보다 조금 낮아짐.

테스트 점수가 정상으로 돌아옴.
>>> 특성을 많이 사용해도 과대적합하지 않아서 좋은 성능을 냄

적잘한 알파값 찾기
알파(alpha)값에 대해 R² 값 그래프 그리기
import matplotlib.pyplot as plt
train_score = []
test_score = []
# 알팍밧을 0.001 ~ 100.0까지 10배씩 늘려가며 릿지 모델을 훈련하고 평가
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
ridge = Ridge(alpha = alpha)
ridge.fit(train_scale, train_target) # 릿지 모델 훈련
# 훈련점수와 테스트점수 저장
train_score.append(ridge.score(train_scale, train_target))
test_score.append(ridge.score(test_scale, test_target))# 그래프 그리기
# alpha_list의 값을 그래프에 동일한 간격으로 표시하기 위해 로그함수로 값 변환
# 0.001 = -3, 0.01 = -2, 0.1 = -1, 1.0 = 0, 10.0 = 1, 100.0 = 2
plt.plot(np.log10(alpha_list), train_score) #훈련 평가 점수 그래프
plt.plot(np.log10(alpha_list), test_score) # 테스트 평가 점수 그래프
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()
- log10(0.001) = -3
- log10(0.01) = -2
- log10(0.1) = -1
- log10(1) = 0
- log10(10) = 1
- log10(100) = 2

왼쪽 : 훈련 세트와 테스트 세트의 점수차이가 큼 == 과대적합
오른쪽 : 훈련 세트와 테스트 세트 모두 낮아짐 == 과소적합
가장 적절한 값은 -1 : 10^-1 = 0.1이 적절한 alpha값
# alpha값이 0.1일 때 최종 목델 훈련하기
ridge = Ridge(alpha = 0.1)
ridge.fit(train_scale, train_target)
# 훈련점수와 테스트점수 저장
print('훈련 점수 :', ridge.score(train_scale, train_target))
print('테스트 점수 :', ridge.score(test_scale, test_target))
2. 라쏘 회귀 모델
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(train_scale, train_target)
print('훈련 점수 :', lasso.score(train_scale, train_target))
print('테스트 점수 :', lasso.score(test_scale, test_target))
train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
lasso = Lasso(alpha = alpha, max_iter = 10000) # max_iter : 훈련 시 반복 횟수
lasso.fit(train_scale, train_target)
# 훈련점수와 테스트점수 저장
train_score.append(lasso.score(train_scale, train_target))
test_score.append(lasso.score(test_scale, test_target))plt.plot(np.log10(alpha_list), train_score) # 훈련 평가점수 그래프
plt.plot(np.log10(alpha_list), test_score) # 테스트 평가점수 그래프
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()
가장 적절한 값은 1 : 10^1 = 10 이 적절한 alpha값
print('훈련 점수 :', lasso.score(train_scale, train_target))
print('테스트 점수 :', lasso.score(test_scale, test_target))
분석 및 비교
| 모델 | 훈련 점수 | 테스트 점수 |
| 릿지 회귀 | 0.9889 | 0.9857 |
| 라쏘 회귀 | 0.9827 | 0.9778 |
릿지 회귀의 성능이 더 좋음
훈련 점수, 테스트 점수 둘 다 높음 : 성능이 좋음
라쏘 회귀보다 테스트 점수가 높아 예측력이 더 좋음
과적합 여부
1. 릿지 회귀의 훈련점수와 테스트 점수가 크게 차이나지 않음 : 과적합 문제 없음.
2. 라쏘 회귀의 훈련 점수와 테스트 점수의 차이도 크지 않지만 릿지보다 성능이 낮음.
로지스틱 회귀(Logistic Regression)
- 이진 분류 문제를 해결하는 머신러닝 알고리즘
선형 회귀와 비슷하지만, 출력값이 0~1 사이의 확률값을 가지도록 변환해서 분류.
선형 회귀는 y = wx + b의 형태로 예측값을 구하지만, 로지스틱 회귀는 확률 값을 출력.(시그모이드 함수 적용)
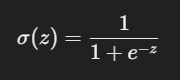
z = wx + b(선형 회귀와 동일)
z값이 작으면 0에 가까워지고, 크면 1에 가까워짐.

데이터 준비
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')
fish.head()
생선 종류 확인을 위한 Species 열의 unique값 추출

Species를 타깃으로 하고, 나머지 컬럼은 입력 데이터로 사용하는 입력 데이터
# 타깃 데이터
fish_target = fish['Species'].to_numpy()
# 입력 데이터 만들기
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
# 입력 데이터 확인
print(fish_input[:5])
훈련 세트, 테스트 세트 만들기
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
fish_input, fish_target, random_state = 42)
표준화 전처리
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
k-최근접 이웃 분류기로 확률 예측
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier(n_neighbors = 3) # 이웃값을 3으로 설정
kn.fit(train_scaled, train_target) # 학습
print('훈련 점수 :', kn.score(train_scaled, train_target))
print('테스트 점수 :', kn.score(test_scaled, test_target))
k-최근접 이웃의 다중 분류
- 타깃 데이터에 2개 이상의 클래스가 포함된 문제를 다중 분류라고 함.
print('학습 클래스 :',kn.classes_) # 모델이 학습한 클래스 확인
print('예측값 :', kn.predict(test_scaled[:5])) # 테스트 데이터 중 앞 5개의 샘플에 대한 예측값 출력
print('실제값 :', test_target[:5]) # 실제 정답 출력
# 테스트 세트 5개 데이터에 대한 확률값 확인하기
# predict_proba()
import numpy as np
proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals = 4)) # 소수 4째 자리까지 표시, 출력 순서는 classes_ 속성과 같음
# 네번째 샘플의 최근접 이웃 확인하기
distances, indexes = kn.kneighbors(test_scaled[3:4])
print(train_target[indexes])
3개의 최근접 이웃을 사용하기 때문에 가능한 확률은 0/3, 1/3, 2/3, 3/3이 전부다.
로지스틱 회귀
z = a*(무게) + b*(길이) + c*(대각선) + d(높이) + e*두께 + f
z 값이 임의의 정수가 되므로 확률로 활용하려면 0 ~ 1 사이의 값으로 표현해야 한다.
>> sigmoid 함수를 사용해서 0 ~ 1 사이의 값으로 변환!
z값이 -5 ~ 5 사이일 때 시그모이드 그래프 그리기
import matplotlib.pyplot as plt
z = np.arange(-5, 5, 0.1) # -5부터 5까지 0.1 간격의 배열 생성
phi = 1 / (1 + np.exp(-z)) # 시그모이드 함수 계산
plt.plot(z, phi)
plt.xlabel('z')
plt.ylabel('phi')
plt.show()
z > 0.5 : 양성
z < 0.5 : 음성
# Bream과 Smelt만 고르기
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]
로지스틱 회귀 모델 훈련



로지스틱 회귀가 학습한 계수 확인

로지스틱 회귀가 학습한 방정식은
z = -0.4038*(무게) -0.5762*(길이) -0.6628*(대각선) -1.0129*(높이) -0.73169*(두께) -2.161
z값 출력

z값을 시그모이드 함수에 통과시켜 확률 얻기
# expit() : Scipy 라이브러리에 시그모이드 함수 활용
from scipy.special import expit
print(expit(decision))
로지스틱 회귀로 다중 분류 수행
# 로지스틱 회귀는 반복적인 알고리즘을 사용해서 학습(max_iter)
# C : 규제 양을 조절하는 값, 기본값 = 1, 값이 작을수록 규제가 커짐.
lr = LogisticRegression(C = 20, max_iter = 1000)
lr.fit(train_scaled, train_target)
print('훈련 점수 :', lr.score(train_scaled, train_target))
print('테스트 점수 :', lr.score(test_scaled, test_target))
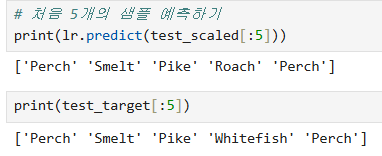
첫 번째(Perch), 두 번째(Smelt), 세 번째(Pike), 다섯 번째(Perch) 샘플은 정확히 예측됨
네 번째 샘플의 실제값은 Whitefish지만 모델은 Roach로 예측 = 오답 발생
# 확률 출력
proba = lr.predict_proba(test_scaled[:5])
print(np.round(proba, decimals = 3))
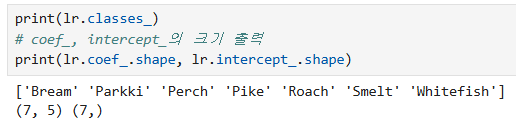
5개의 특성에 대해 각 클래스 별로 7번 z값을 계산한다.
# 첫번째 5개의 z값 산출
decision = lr.decision_function(test_scaled[:5])
print(np.round(decision, decimals=2))
소프트맥스 함수를 이용해서 7개의 z값을 한번에 확률로 변환하기
from scipy.special import softmax
proba = softmax(decision, axis = 1)
print(np.round(proba, decimals = 3))
확률적 경사 하강법(SGDClassifier)
- 손실함수를 최소화하기 위해 가중치를 조정함녀서 최적값을 찾는 알고리즘
- 모델이 예측한 값과 실제 값의 차이를 줄이는 방향으로 가중치를 학습.
- 경사 : 손실함수의 기울기(변화율)
- 학습률 : 한 번에 가중치를 얼마나 이동할지 결정.


SGDClassifier를 사용한 훈련
# 2개의 매개변수 :
# loss : 손실함수 종류 지정(log_loss)
# max_iter : 수행 반복(에포크) 횟수 지정(10)
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log_loss', max_iter = 10, random_state = 42)
sc.fit(train_scaled, train_target) # 학습
print('훈련 점수 :', sc.score(train_scaled, train_target))
print('테스트 점수 :', sc.score(test_scaled, test_target))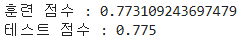
SGDClassifier를 사용한 점진적 학습
sc.partial_fit(train_scaled, train_target)
print('훈련 점수 :', sc.score(train_scaled, train_target))
print('테스트 점수 :', sc.score(test_scaled, test_target))
에포크의 횟수에 따라 모델의 정확도 그래프 그리기
# 300번의 에포크 실행
import numpy as np
sc = SGDClassifier(loss='log_loss', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
for _ in range(0,300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))- SGDClassifier(loss='log_loss', random_state=42) : 확률적 경사 하강법 기반의 로지스틱 회귀 모델
- loss = 'log_loss' : 로지스틱 회귀 모델 사용
- random_state : 랜덤성을 고정해서 재현 가능성 확보
- classes = np.unique(train_target) : 훈련 데이터의 고유 클래
- train_target : 고유 클래스 목록 저장
- partial_fit()을 사용할 때 classes를 지정해야 온라인 학습이 가능
- partial_fit() : 한번에 모든 데이터를 학습하지 않고, 한 번의 반복(에포크)마다 일부 데이터만 학습하는 방식
- partial_fit(train_scaled, train_target, classes=classes)
- train_scaled : 훈련 데이터
- train_target : 정답
- classes = classes : 모델이 모든 클래스를 기억하도록 설정 (필수)
- partial_fit(train_scaled, train_target, classes=classes)
# 그래프 그리기
import matplotlib.pyplot as plt
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
파란색 선 : 훈련 세트 그래프
주황색 선 : 테스트 세트 그래프
초반 : 과소적합, 100 이후 : 점수가 조금씩 벌어짐
100번의 반복(에포크)이 적절한 반복 횟수임
# tol - 일정 에포크(반복) 동안 성능이 향상되지 않으면 훈련을 자동으로 멈추는 옵션
sc = SGDClassifier(loss='log_loss', max_iter=100, random_state=42, tol=None)
sc.fit(train_scaled, train_target)
print('훈련 점수 :', sc.score(train_scaled, train_target))
print('테스트 점수 :', sc.score(test_scaled, test_target))
'Python' 카테고리의 다른 글
| [Python] 트리 앙상블 (0) | 2025.03.11 |
|---|---|
| [Python] 머신러닝 (3) (0) | 2025.03.10 |
| [Python] 머신러닝 (1) (0) | 2025.03.05 |
| [Python] 클래스(Class) (0) | 2025.03.04 |
| [Python] 람다 표현식 (0) | 2025.03.02 |