[Python] 머신러닝 (1)

Python

[Python] 머신러닝 (1)

orin602 2025. 3. 5. 14:10

KNN(K-Nearest Neighbors Classfier) : 새로운 데이터 포인트의 클래스(label)를 예측할 때,

가장 가까운 K개의 이웃(데이터 포인트)의 클래스를 참고해서 결정하는 알고리즘.

KNN의 특징
- 거리 기반 알고리즘
- 데이터가 많아질수록 연산 비용 증가(비효율적)
- 학습 과정이 거의 없음(Lazy Leaning)
- 데이터 분포가 명확하면 강력한 성능 발휘
KNN의 동작 원리
- 새로운 데이터 포인트가 주어지면 기존 데이터와의 거리를 계산
- 가장 가까운 K개의 이웃을 선택
- 이웃들의 클래스 중 가장 많이 등장하는 클래스를 새로운 데이터의 클래스로 예측
장점
- 이해하고 구현하기 쉽다
- 학습 시간이 거의 없다
- 적절한 K값 설정 시 높은 성능
단점
- 데이터가 많아지면 거리 계산 비용 증가
- K값 설정이 성능에 큰 영향을 미침
- 차원의 저주(Curse of Dimensionality)에 취약

KNN의 주요 하이퍼파라미터

파라미터	설명
n_nighbors	참고할 이웃의 개수(K값) (기본값은 5)
metric	거리 측정 방법 (예: euclidean, manhattan, minkowski)
weights	이웃의 가중치 (예: uniform=평균, distance=가까운 점에 더 큰 가중치)
algorithm	까운 이웃을 찾는 방법 (auto, ball_tree, kd_tree, brute)

K값(K-Neighbors) 선택 방법
- K가 너무 작음 : 모델이 데이터에 과적합됨
- K가 너무 큼 : 모델이 너무 일반화되어 정확도가 낮아짐
- 일반적으로 홀수를 사용하여 다수결 충돌을 방지
K 값은 데이터에 따라 최적값이 다르므로, 교차 검증(Cross Validation)을 사용하여 적절한 K 값을 찾는 것이 좋습니다.

# 예제 데이터 준비
# 도미 데이터의 길이와 무게

bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]

bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]

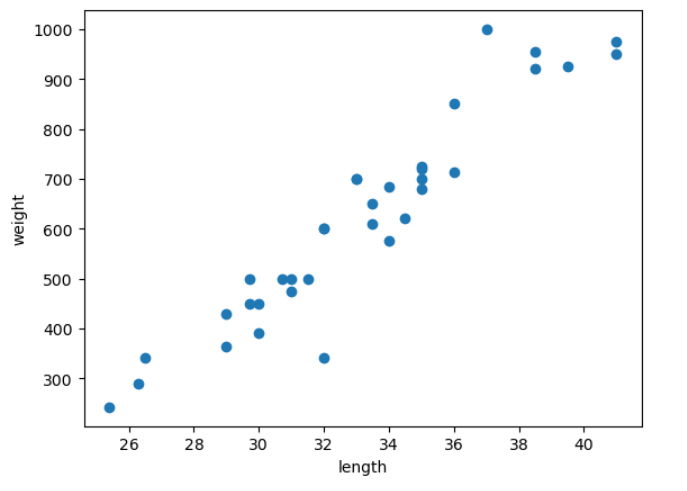
도미 데이터로 산점도 그리기

import matplotlib.pyplot as plt

plt.scatter(bream_length, bream_weight) # scatter : 산점도
plt.xlabel('length') # x축 : 길이
plt.ylabel('weight') # y축 : 무게
plt.show()

import matplotlib.pyplot as plt : Matplotblib은 파이썬에서 그래프를 그리는 라이브러리로 다양한 차트(산점도, 선 / 막대 그래프 등)를 쉽게 만듬.
- pyplot은 Matplotlib에서 간단하게 그래프를 그릴 수 있도록 도와주는 모듈
plt.scatter(x, y) : x와 y의 데이터르 점으로 표시하는 선점도를 그린다.
plt.xlabel(), plt.ylabel() : 각각 x축과 y축에 이름 설정.
plt.show() : 그래프 출력

# 빙어 데이터 준비
# 도미 데이터는 35마리 길이(cm), 무게(g)..
# 빙어 데이터는 14마리   //    ,   //

smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8,
                11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]

smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9,
                9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

도미와 빙어의 데이터를 하나의 산점도로 그리기

plt.scatter(bream_length, bream_weight)
plt.scatter(smelt_length, smelt_weight)
plt.title('bream vs smelt') # 그래프 제목
plt.xlabel('length')
plt.ylabel('weight')
plt.grid(True) # 격자 추가
plt.show()

도미와 빙어 데이터 합치기

length = bream_length + smelt_length
weight = bream_weight + smelt_weight

fish_data = [[l, w] for l, w in zip(length, weight)]
fish_target = [1] *35 + [0] * 14

fish_data = [[l, w] for l, w in zip(length, weight)]
- zip(length, weight) : length와 weight를 묶어서 (길이, 무게) 형태의 튜플 생성
- l =길이, w=무게
- [[l, w] for l, w in zip(length, weight)] : [길이, 무게] 형태의 2차원 리스트로 변환
fish_target = [1] *35 + [0] * 14
- 도미 데이터(총 35개): 1
- 빙어 데이터(총 14개): 0

K-최근점 이웃(KNeighborsClassifier) 알고리즘을 통한 학습

- 어떤 데이터에 대한 답을 구할 떄 주위의 가장 가까운 데이터를 보고 다수를 차지하는 것을 정답으로 정함.

from sklearn.neighbors import KNeighborsClassifier

# import한 KNeighborsClassifier 클래스 객체 생성
kn = KNeighborsClassifier()

#fish_data와 fish_target을 전달해서 학습시키기
kn.fit(fish_data, fish_target)

KNeighborsClassifier : 사이킷런(scikit-learn)에서 제공하는 KNN 분류기
kn 은 KNeighborsClassifier()의 객체(기본값 k=5(가장 가까운 5개의 이웃을 참고)로 설정됨)
fit(fish_data, fish_target ) : 모델 학습
- fish_data : 입력 데이터(길이, 무게)
- fish_target : 출력 데이터 (도미=1, 빙어=0)

훈련 평가

score() : 사이킷런에서 모델 평가 메서드
- 결과값 = 정확도
- 1.0 : 정확도(accuracy)가 100%라는 의미.

새로운 데이터 예측하기

kn.predict([[30, 555]])
- 길이 30, 무게 555인 물고기의 종류 예측
- 기본값(k=5) : 가장 가까운 5개의 데이터를 찾아 해달 라벨(도미=1, 빙어=0)의 다수 선택
- 데이터 간 거리를 기준으로 가장 가까운 물고기 5마리를 찾음
array([1])
- 결과가 1이면 도미
- 결과가 0이면 빙어

훈련 세트와 테스트 세트

# 도미와 빙어 데이터를 하나의 리스트로 준비

fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0,
              9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]

fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0,
               500.0, 500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0,
               620.0, 680.0, 700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0,
               975.0, 950.0,6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2,
               19.7, 19.9]

# 길이, 무게 데이터를 합쳐서 하나의 리스트로 만들기
fish_data = [[l, w] for l, w in zip(fish_length, fish_weight)]
fish_target = [1] * 35 + [0] * 14

# k-최근접 이웃 클래스 객체 생성
kn = KNeighborsClassifier() # 기본값 k=5

# fish_data의 n번째 샘플 출력
print(fish_data[7]) # 7번째 샘플 출력

훈련 세트와 테스트 세트 선택

# 훈련 세트로 입력값 0~34번 인덱스 사용
train_input = fish_data[:35]
train_target = fish_target[:35]

# 테스트 세트로 35~ 마지막 인덱스 사용
test_input = fish_data[35:]
test_target = fish_target[35:]

학습 및 평가

# 학습은 훈련 데이터로 수행
kn.fit(train_input, train_target)

# 평가는 테스트 테이터로 수행
kn.score(test_input, test_target)

샘플링 편향 : 훈련 세트에 빙어의 데이터가 존재하지 않아서 옳바르게 분류할 수 없음.

도미와 빙어 데이터 섞기

# 파이썬 리스트를 넘파이 배열로 변환
import numpy as np

input_arr = np.array(fish_data)
target_arr = np.array(fish_target)

input_arr

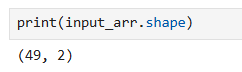
.shape : 행(row)과 열(column)의 개수 확인

>>> (49, 2) : 49개 행(데이터가 49개), 2개 열(길이, 무게 = 두 개의 속성)

인덱스를 섞고 훈련세트와 테스트세트 준비

np.random.seed(42)
index = np.arange(49)
np.random.shuffle(index)
index

np.random.seed(42)
- 랜덤 결과를 항상 동일하게 유지.
- 동일한 코드를 실행할 때마다 같은 순서로 섞음.
np.arange(49)
- 0 ~ 48 까지의 숫자를 순서대로 저장한 배열 생성.
np.random.shuffle(index)
- " index " 배열을 무자위로 섞음.
- " index "의 원소 값(0 ~ 48)은 그대로 유지, 순서만 랜덤으로 변경.

# 35개의 데이터를 훈련세트로 만들기
train_input = input_arr[index[:35]]
train_target = target_arr[index[:35]]
print('원본 데이터 :', input_arr[13], '셔플 데이터 :', train_input[0])

# 나머지 데이터를 테스트세트로 만들기
test_input = input_arr[index[35:]]
test_target = target_arr[index[35:]]

셔플 후 데이터 확인하기

import matplotlib.pyplot as plt

plt.scatter(train_input[:, 0], train_input[:, 1], label='train')	# 1
plt.scatter(test_input[:, 0], test_input[:, 1], label='test')		# 2
plt.legend(loc='lower right')						# 3
plt.xlabel('length')							# 4
plt.ylabel('weight')							# 5
plt.show()								# 6

훈련 데이터 산점도
1. train_input[:, 0]: x축 (길이) → 모든 행(:)에서 첫 번째 열(길이) 선택
2. train_input[:, 1]: y축 (무게) → 모든 행에서 두 번째 열(무게) 선택
3. label='train': 범례 추가 (훈련 데이터 표시용)
테스트 데이터 산점도
1. test_input[:, 0]: x축 (길이)
2. test_input[:, 1]: y축 (무게)
3. label='test': 범례 추가 (테스트 데이터 표시용)
범례 추가(오른쪽 아래)
1. 범례(legend) 추가 → 훈련 데이터와 테스트 데이터를 구분하기 위함
2. loc='lower right': 오른쪽 아래에 범례 표시
x축 이름 설정
y축 이름 설정
그래프 표시

k-최근접 이웃 모델 훈련

fit(훈련 데이터, 정답 데이터)으로 모델 학습
- train_input : 훈련 데이터(길이, 무게 등 특징)
- train_target : 훈련 데이터의 정답(도미=1, 빙어=0)
score(테스트 데이터, 테스트 정답)으로 모델 성능 평가
- test_input : 테스트 데이터 (길이, 무게)
- test_target : 실제 정답 (1=도미, 0=빙어)
- 결과 1.0 : 모델의 정확도 (0~1 사이 값, 1에 가까울수록 성능이 좋음)

예측 결과 확인

predict(입력 데이터)로 새로운 데이터 예측
- 결과값 : 예측된 정답 리스트(1 = 도미, 0 = 빙어)
test_target은 테스트 데이터의 실제 정답
- kn.predict(test_input) 결과와 비교하여 모델이 얼마나 잘 예측했는지 확인

데이터 전처리

- 머신러닝 모델의 성능을 높이기 위해 반드시 필요한 과정.

데이터 준비

# 데이터 준비

fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0,
              9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]

fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0,
               500.0, 500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0,
               620.0, 680.0, 700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0,
               975.0, 950.0,6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2,
               19.7, 19.9]

column_stack() 함수 활용하기

1차원 배열 또는 2차원 배열을 열(column)단위로 병합하는 함수.

# column_stack() 사용하기
# fish_length와 fish_weight를 엮어 fish_data 생성
fish_data = np.column_stack((fish_length, fish_weight))
print(fish_data[: 5]) # 0 ~ 4 번째 데이터 확인

타겟 데이터 만들기

fish_target = np.concatenate((np.ones(35), np.zeros(14)))
print(fish_target)

np.ones(35) : 1이 35개 들어있는 배열 생성.
np.zeros(14) : 0이 14개 들어있는 배열 생성.
np.concatenate() : 두 개의 배열을 합쳐 하나의 1차원 배열 생성.
- np.concatenate((배열1, 배열2, ...), axis = 0)
  - axis = 0 : 기본값, 행 기준 연결
  - axis = 1 : 열 기준 연결

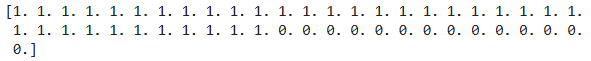
훈련 세트와 테스트 세트로 나누기

# train_test_split() : 사이킷런에서 훈련 세트와 테스트 세트로 분류하는 기능
# 기본적으로 25%를 테스트 세트로 떼어냄
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_data, fish_target,
                                                                      random_state = 42)

train_test_split(fish_data, fish_target, random_state=42)
- fish_data : 입력 데이터(x)
- fish_target : 정답 데이터(y)
- random_state = 42 : 랜덤 시드를 고정해 실행할 때마다 같은 결과가 나오도록 설정.
  (42는 그냥 많이 쓰는 값이며, 다른 숫자를 넣어도 됨)
- 반환 값: train_input, test_input, train_target, test_target (훈련/테스트 데이터 & 정답)

앞에서 테스트한 데이터는 35개가 훈련 세트, 14개가 테스트 세트였지만, 지금은 훈련세트가 36개, 테스트 세트가 13개

>> 앞에서의 기준에 맞추기 위해 stratify 속성 사용 : target data의 갯수에 맞게 훈련 세트와 테스트 세트 분류

train_input, test_input, train_target, test_target = train_test_split(fish_data, fish_target,
								stratify=fish_target, random_state=42)

print(test_target)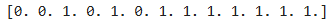

k-최근접 이웃 모델링 훈련

kn = KNeighborsClassifier()
kn.fit(train_input, train_target) # 학습
kn.score(test_input, test_target) # 평가

산점도로 이상한 데이터 확인하기

plt.scatter(train_input[:, 0], train_input[:, 1]) # 훈련용 데이터 표시
plt.scatter(25, 150, marker = '^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

샘플에서 가장 가까운 이웃 찾기

# kneighbors() : k-최근접 이웃 알고리즘에서 입력 데이터와 가장 가까운 k개의 이웃을 찾는 함수
# kn.kneighbors()
distances, indexes = kn.kneighbors([[25, 150]])
print(distances)
print(indexes)

[[25, 150]] : 길이 25, 무게 150인 데이터
기본값으로 n_neighbors=5 : 5개의 최근접 이웃 반환
disstances : 이웃과의 거리
indexes : 이웃 데이터의 인덱스

index 배열을 사용해서 산점도 그리기

plt.scatter(train_input[:, 0], train_input[:, 1])
plt.scatter(25, 150, marker = '^')
plt.scatter(train_input[indexes, 0], train_input[indexes, 1], marker = 'D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

train_input은 훈련 데이터의 입력 특성(길이와 무게)
trian_input[:, 0]은 첫 번째 특성 : 길이
train_input[:, 1]은 두 번째 특성 : 무게
train_input[indexes, 0]와 train_input[indexes, 1]은 indexes 배열에 포함된 훈련 데이터의 인덱스를 기준으로 가장 가까운 K개의 이웃의 특성(길이와 무게)

샘플에 가까운 5개의 물고기 중 도미(1)는 한마리

# x축읜 범위를 y축과 동일하게 0 ~ 1000으로 맞추기
plt.scatter(train_input[:, 0], train_input[:, 1])
plt.scatter(25, 150, marker = '^')
plt.scatter(train_input[indexes, 0], train_input[indexes, 1], marker = 'D')
plt.xlim(0, 1000) # x축 범위 지정
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

위의 그래프처럼 길이, 무게의 범위가 다른 것을 스케일이 다르다고 함.

>> 데이터를 표현하는 기준이 다르면 예측이 옳바르게 할 수 없음.

>>>> 표준화 전처리 과정!

# 표준화 전처리 과정
# 표준 점수 = (입력값 - 평균) / 표준 편차
mean = np.mean(train_input, axis = 0) # 평균
std = np.std(train_input, axis = 0) # 표준 편차

print('평균 :', mean, '\n표준 편차 :', std)

# 원본 데이터에서 평균을 빼고 표준 편차로 나누기(브로드캐스팅)
train_scaled = (train_input - mean) / std

plt.scatter(train_scaled[:, 0], train_scaled[:, 1])
plt.scatter(25, 150, marker = '^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

# 예측 데이터를 표준 점수로 변환해서 산점도 그리기
new = ([25, 150] - mean) / std
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

표준 점수로 계산된 데이터셋으로 k-최근접 이웃 모델 훈련

예측 데이터로 kneighbors() 함수를 사용해 k-최근접 이웃을 구해 산점도 그리기

distances, indexes = kn.kneighbors([new])
plt.scatter(train_scaled[:, 0], train_scaled[:, 1])
plt.scatter(new[0], new[1], marker = '^')
plt.scatter(train_scaled[indexes, 0], train_scaled[indexes, 1], marker = 'D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

처음 샘플의 이웃을 찾았을 때와는 다르게 모두 도미(1)로 나옴

K-최근접 이웃 회귀(K-Nearest Neighbors Regression)

- 기본적으로 KNN 분류는 주어진 데이터가 어떤 클래스에 속할지 예측하는 분류에 사용되지만, 회귀는 연속적인 수치 값을 예측하는데 사용된다.

- 회귀에서 KNN은 주어진 입력 값에 대해 가장 가까운 k개의 이웃의 평균값 또는 중앙값을 이용해 예측한다.

>>> 가장 가까운 데이터 포인터들의 출력 값들을 평균값 또는 중간값을 구해 예측값으로 사용.

장점
- 간단하고 직관적 : KNN 회귀는 매우 직관적이고 이해하기 쉬운 방법이다.
- 비모수적 : 데이터의 분포를 가정하지 않으므로 모수 모델이 아닌 비모수적 모델이다.(데이터에 대한 특별한 가정 없이도 작동함)
- 학습 속도가 빠름 : KNN은 훈련 시 모델을 학습하지 않는다.(대신 예측 시 데이터 기반으로 계산을 수행)
단점
- 고차원 데이터에서 성능 저하 : 차원의 저주에 취약하다.
- 데이터가 많을수록 예측 속도 저하 : 데이터 포인트가 많을수록 예측 시 계산량이 증가하여 예측 시간이 오래 걸린다.
- 이웃 개수(k)의 선택 : k값에 대한 하이퍼파라미터 튜닝이 중요.

데이터 준비

import numpy as np

perch_length = np.array(
    [8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 
     21.0, 21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 
     22.5, 22.7, 23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 
     27.3, 27.5, 27.5, 27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 
     36.5, 36.0, 37.0, 37.0, 39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 
     40.0, 42.0, 43.0, 43.0, 43.5, 44.0]
     )
perch_weight = np.array(
    [5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 
     110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 
     130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 
     197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 
     514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 
     820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 
     1000.0, 1000.0]
     )

산점도 그리기

import matplotlib.pyplot as plt

plt.scatter(perch_length, perch_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

훈련 세트와 테스트 세트로 나누기

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(
    perch_length, perch_weight, random_state = 42)
print(train_input)
print(train_target)

k-최근접 이웃 회귀 알고리즘을 사용해 훈련 및 평가

# k-최근접 이웃 회귀 클래스 : KNeighborsRegressor
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()
knr.fit(train_input, train_target)

테스트 점수 확인하기

회귀 알고리즘의 평가

분류 : 테스트 세트에 있는 샘플을 정확히 분류한 갯수의 비율 = 정확도

회귀 : 정확한 숫자를 맞추는 것이 불가능 = 결정계수로 평가

(결정계수 : 회귀 모델이 데이터의 변동성을 얼마나 잘 설명하는지를 나타낸다)

1에 가까울수록 모델이 타깃을 잘 예측한 것이고, 0에 가까울수록 모델이 예측에 실패한 것

평균 절대값 오차(Mean Absolute Error, MAE)구하기

# 예측한 값이 어느 정도 타깃값에서 벗어났는지 확인 : mean_absolute_error
from sklearn.metrics import mean_absolute_error

# 테스트 세트에 대한 예측
test_prediction = knr.predict(test_input)

# 테스트 세트에 대한 평균 절대값 오차 계산
mean_error = mean_absolute_error(test_target, test_prediction) # 타겟값과 예측값 비교

print(mean_error)

평균적으로 19.16정도 타깃값과 다르다.

훈련 세트 평가와 테스트 세트 평가

# 훈련 세트 평가
print('훈련 세트 평가 :', knr.score(train_input, train_target))

# 테스트 세트 평가
print('테스트 세트 평가 :', knr.score(test_input, test_target))

과소적합(Underfitting) vs 과대적합(Overfitting)
- 과소적합 : 모델이 훈련 데이터를 충분히 학습하지 못해 예측 성능이 낮은 경우.
  - 해결 방법
    - 더 복잡한 모델 사용
    - 훈련 데이터를 더 많이 사용
    - 특성을 추가해 모델 개선
- 과대 적합 : 모델이 훈련 데이터에 너무 잘 맞춰져 테스트 데이터에 대한 예측 성능이 떨어지는 경우
  - 해결 방법
    - 모델의 복잡도 줄이기
    - 정규화 기법 사용
    - 훈련 데이터의 양을 늘리거나 교차 검증을 통해 모델 튜닝

훈련 세트의 평가점수보다 테스트 세트의 평가점수가 높다 = 과소적합

# 이웃의 기본값(k)을 수정하기
# 과대적합일 경우 k값 증가, 과소적합일 경우 k값 감소
knr.n_neighbors = 3

# 모델 다시 훈련
knr.fit(train_input, train_target)
print('훈련 세트 평가 :', knr.score(train_input, train_target))

print('테스트 세트 평가 :', knr.score(test_input, test_target))

산점도를 그려 k값을 변경하여 훈련하기

knr = KNeighborsRegressor()

# 농어의 길이를 5에서 45까지 바꿔가며 예측
x = np.arange(5, 45).reshape(-1, 1)

# 이웃값 k = 1, 5, 10일 때 예측 결과 그리기
for n in [1, 5, 10]:
    knr.n_neighbors = n # 이웃값 변경
    knr.fit(train_input, train_target) # 학습
    prediction = knr.predict(x) # 위에서 정한 x 범위에 대해 예측

    # 훈련 세트와 예측 결과 그리기
    plt.scatter(train_input, train_target)
    plt.plot(x, prediction)
    plt.title('n_neighbors = {}'.format(n))
    plt.xlabel('length')
    plt.ylabel('weight')
    plt.show()

k 값이 1일 때

예측값이 불규칙적임

k 값이 5일 때

예측값이 좀 더 부드럽고, 안정적임

k 값이 10일 때

예측값이 더 부드럽고 일관되게 나타남

선형 회귀(Linear Regression)

- 독립 변수(x)와 종속 변수(y)간의 선형적인 관계를 모델링하는 회귀 분석 방법.

장점
- 단순하고 이해하기 쉬움 : 선형 회귀는 직관적이고 구현하기 쉬운 모델이다.
- 속도와 효율성 : 계산량이 적고, 빠르게 학습할 수 있어 대규모 데이터셋에서 유용하게 사용된다.
- 해석 가능성 : 결과인 회귀 계수는 각 입력 변수의 중요도를 직관적으로 해석할 수 있다.
한계
- 선형성 가정 : 데이터가 비선형 관계를 가질 경우, 선형 회귀는 잘 작동하지 않을 수 있다.
- 이상치(Outlier)에 민감 : 이상치가 존재하면 모델의 성능이 크게 저하될 수 있다.
- 다중 공선성(Multicolinearity) : 입력 변수 간에 강한 상관관계가 있을 때 회귀 계수가 불안정해지고, 모델이 과적합될 수 있다.

위에서 k-최근접 이웃 회귀의 한계

- 훈련용 농어 데이터는 길이가 5 ~ 45인 데이터를 가지고 훈련

>> 45를 초과하는 데이터에 대해서는 옳바르게 예측을 못함.

# 이웃 회귀에서 사용한 데이터 준비

perch_length = np.array(
    [8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 
     21.0, 21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 
     22.5, 22.7, 23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 
     27.3, 27.5, 27.5, 27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 
     36.5, 36.0, 37.0, 37.0, 39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 
     40.0, 42.0, 43.0, 43.0, 43.5, 44.0]
     )

perch_weight = np.array(
    [5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 
     110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 
     130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 
     197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 
     514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 
     820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 
     1000.0, 1000.0]
     )

# 훈련 세트와 테스트 세트 나누기
train_input, test_input, train_target, test_target = train_test_split(
    perch_length, perch_weight, random_state = 42)

# 훈련 세트와 테스트 세트를 2차원 배열로 변환하기
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)

45를 초과하는 농어의 무게 예측하기

산점도를 그려 확인하기

distances, indexes = knr.kneighbors([[50]])

plt.scatter(train_input, train_target)
plt.scatter(train_input[indexes], train_target[indexes], marker = 'D')

# 50cm 농어 데이터 그리기
plt.scatter(50, 1033, marker = '^')
plt.scatter(60, 1033, marker = '^')

plt.xlabel('length')
plt.ylabel('weight')
plt.show()

45를 초과하는 길이의 농어는 모두 1033.33333

선형 회귀로 예측하기

이웃회귀의 예측(1033.3333) vs 선형회귀의 예측(1241.8386)

LinearRegression이 찾은 계수와 절편값 확인하기

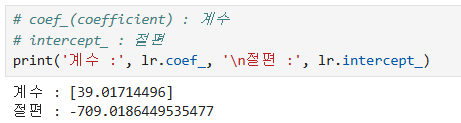
coef_(계수) : 선형 회귀 모델의 회귀 계수.
- 각 독립 변수에 대해 학습된 계수들이며, 모델이 입력 변수에 얼마나 중요한 영향을 미치는지를 나타냅니다.
intercept_(절편) : 회귀 직선이 y축과 만나는 절편
회귀 계수 39.0171로 가중치 부여
절편은 -709.02로 회귀 직선이 y축과 만나는 값

훈련 세트의 산점도 그리기

plt.scatter(train_input, train_target)

# 15~50 까지의 1차 방정식 그래프
plt.plot([15, 50], [15 * lr.coef_ + lr.intercept_, 50 * lr.coef_ + lr.intercept_])

plt.scatter(50, 1241.8, marker = '^')
plt.show()

15 * lr.coef_ + lr.intercept_와 50 * lr.coef_ + lr.intercept_는 각각 x값이 15일 때와 50일 때의 예측된 y값

훈련 세트와 테스트 세트 평가

1. 모델 측정 결과 과적합 문제

2. 농어의 길이가 줄어들수록 0g 이하로 내려가야되는 현상

>> 그래프는 왼쪽 위로 구부러진 형태

다항 회귀 (Polynomial Regression)

- 선형 회귀의 확장으로, 데이터가 비선형 관계를 가질 때 모델링을 위해 사용.

다 회귀 특징
- 고차항 추가 : 데이터의 변화를 보다 정확하게 반영하기 위해 고차항을 추가한다.
- 비선형성 : 데이터가 비선형적인 패턴을 가질 때 해결이 가능하다.
모델링 절차
- 특성 변환 : 기존의 입력 데이터를 다항식으로 변환해야한다.
- 선형 회귀 모델 훈련 : 변환된 특성을 이용해 선형 회귀 모델을 훈련시킨다.
장점
- 비선형 데이터에도 적합
- 단순한 선형 모델을 확장하여 복잡한 데이터를 모델링할 수 있다.
단점
- 차수를 너무 높게 설정하면 과적합의 위험이 크다.
- 차수에 따라 모델이 매우 복잡해져서 해석이 어려워질 수 있다.
- 다항 특성의 수가 많아지면 계산량이 증가하고 모델이 복잡해진다.

농어의 길이의 제곱항을 추가해서 훈련

train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))
print(train_poly.shape, test_poly.shape)

train_poly를 이용해 선형회귀 모델 다시 훈련하기

lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50 ** 2, 50]]))

선형 회귀로 학습한 모델보다 더 높은 값으로 예측

훈련 세트의 산점도에 학습한 모델의 차트 그리기

# 입력 데이터 구간 : 15~50cm
point = np.arange(15,50)

# 훈련 세트 산점도
plt.scatter(train_input, train_target)

# 15에서 49까지의 학습한 모델의 그래프 그리기
plt.plot(point, 1.0143 * point**2 - 21.557 * point + 116.050)

# 50cm의 농어 데이터
plt.scatter(50, 1574, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

여전히 테스트에 대한 점수가 높아 과소적합 문제가 있지만, 훨씬 더 좋은 모델을 찾을 수 있음.

'Python' 카테고리의 다른 글

[Python] 머신러닝 (3) (0)	2025.03.10
[Python] 머신러닝 (2) (0)	2025.03.08
[Python] 클래스(Class) (0)	2025.03.04
[Python] 람다 표현식 (0)	2025.03.02
[Python] 추천 시스템(2) (0)	2025.03.01

현재글[Python] 머신러닝 (1)

백엔드 개발자 꿈나무의 코딩 기록

백엔드 개발자 꿈나무

spring mvc, javascript, crud, 웹개발, 머신러닝, 댓글 기능 구현, Spring Boot 프로젝트, Python, SweetAlert2, html, SpringBoot, JPA, spring boot, Oracle DB, 백엔드 개발, Thymeleaf, SpringBoot 프로젝트, ajax, 웹 개발, Java,

Today :
Yesterday :

백엔드 개발자 꿈나무의 코딩 기록